Documentation Home Page ◇ HYPERSIM Home Page
Pour la documentation en FRANÇAIS, utilisez l'outil de traduction de votre navigateur Chrome, Edge ou Safari. Voir un exemple.
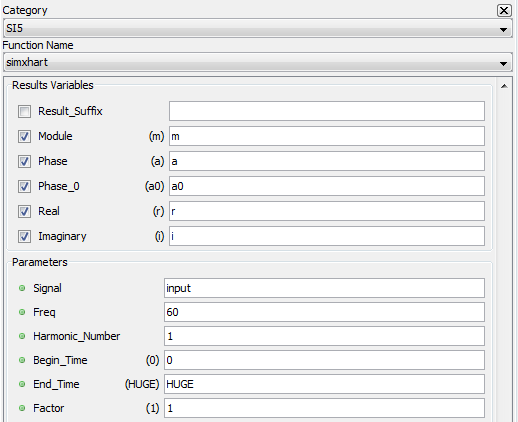
Advanced | SIMXHART
HARMONIC MAXIMUM – [SIMXHART]
Computes the maximum of the amplitudes of a given harmonic.
CATEGORY
Advanced
DESCRIPTION
The function allows computing the maximum of the amplitudes of a given harmonic in a moving window over a signal. This window is equal to the length of a cycle with respect to the fundamental frequency. This function computes module (amplitude) and angle (phase) for the symmetric components and its real and imaginary components.
If the number of samples to establish the length of a cycle is greater than the number of samples found between the starting and ending times of the sequence, then the length of the window used is equal to the number of samples between the starting and ending times (in other words ending time starting-time).
RESULT VARIABLES AND PARAMETERS
| Module (m) | Maximum of module (or amplitude) for the symmetric components of a harmonic. It is computed for each window moving over the signal, multiplied by the absolute value of the factor. |
| Phase (a) | Angle a (or phase) of the symmetric component sequence associated with the maximum module found. Value is between -180 and 180 degrees [°]. Since the module is multiplied by the absolute value of the factor, the phase is modified if the multiplying factor is negative. In this case, 180 degrees are added to the phase. |
| Phase (a0) | Angle a0 (or phase) of the symmetric component sequence associated with the maximum module found. Value is between 0 and 360 degrees [°]. |
| Real (r) | Real part r of the required symmetric component sequence (m * cos(a)). |
| Imaginary (i) | Imaginary part i of the required symmetric component sequence (m * sin(a)). |
| Signal | Input signal to perform analysis |
| Freq | Fundamental frequency of the signal in Hertz [Hz], normally compute with the sifreq function. This fundamental frequency in hertz serves to establish the length of time the window moves over the analyzed signal. In fact, this window is equal to one cycle (in number of samples). lfen = rate/ freq [samples]. |
| Harmonic number | Number of harmonic to compute.
|
| Begin_time | Time at which the analysis of a signal must start. This time is expressed in milliseconds [ms]. This value must be greater than 0 and lower than the size of the acquisition buffer. The default value is 0. |
| End_time | Time at which the analysis of a signal must end. This time is expressed in milliseconds [ms]. The value of this time must be larger than the specified begin_time and smaller than the duration of the test. Use the “HUGE” value to specify the end of the test. The default value is HUGE. Note : The begin_time and end_time specified for the calculation of the harmonics must be the same as those used in the sifreq sequences used to compute the fundamental frequency. |
| Factor | Multiplying factor for the results generated by the function. The default value of the multiplying factor is 1.0 and has no effect on the results. |
SYNTAX
[m, a, a0, r, i] = simxhart( input, 60, 1, 0, HUGE, 1)
CHARACTERISTICS
Data type support
Double Floating point
EXAMPLE
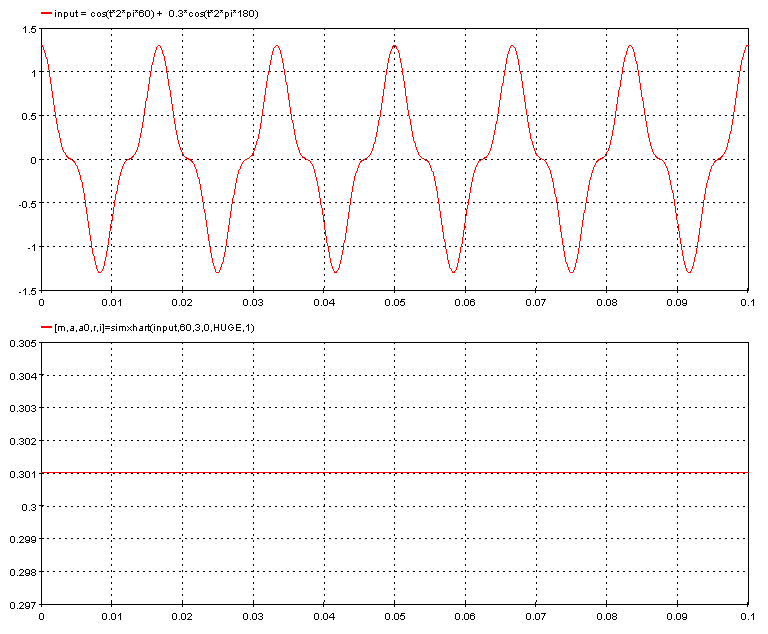
In the following example, the function compute amplitude maximum of the third harmonic components of a signal.
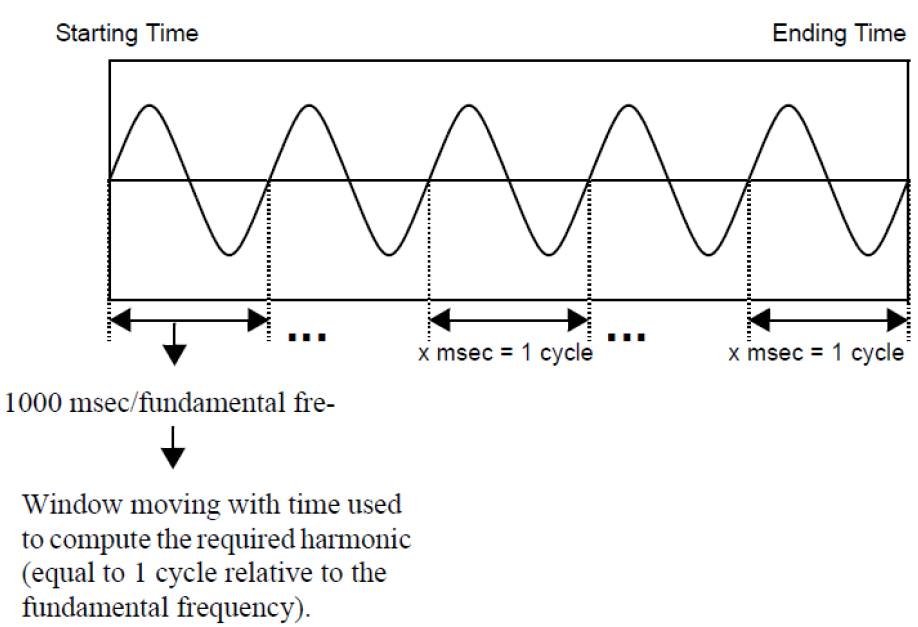
The following diagram shows a window moving over a signal. The method used to compute the length of the window is also described.
The module of the harmonic is computed for each window from the start to the end of the limits and the function returns the maximum of the computed.
Let:
- nbech: number of samples to analyze for the signal
- lfen: number of samples in a window
- nbfen: number of windows for which the calculations are made
Then:
- nbfen=nbech-lfen+1
This set of points is used to find the maximum.
OPAL-RT TECHNOLOGIES, Inc. | 1751, rue Richardson, bureau 1060 | Montréal, Québec Canada H3K 1G6 | opal-rt.com | +1 514-935-2323