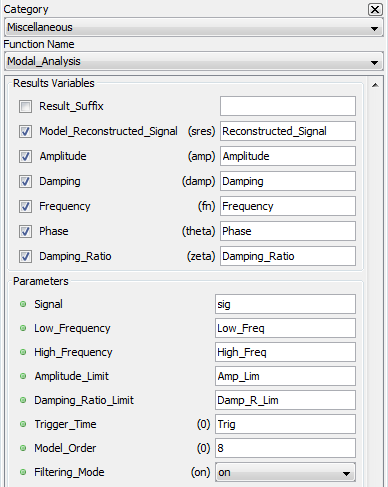
Misc. | AMOD

MODAL ANALYSIS – [AMOD]
This function outputs modal analysis of a single input signal.

CATEGORY
Miscellaneous

DESCRIPTION
The modal analysis returns the dynamic parameters containing the amplitude, damping, frequency, phase shift and damping ratio of each complex mode identified in the input signal by processing it through an ERA/Prony algorithm method.
To return the modal analysis results, the analyzed input signal is presumed as the impulse-response of a black-box dynamic state-space system. The system identification of this dynamic system is obtained by applying the Eigensystem realization algorithm (ERA) based on Hankel matrices, singular value decomposition and Markov parameters calculation to the input signal. From this system identification, the Prony approach algorithm is then applied to obtain the dynamic parameters based on the system’s equation and residual terms calculation.

RESULT VARIABLES AND PARAMETERS

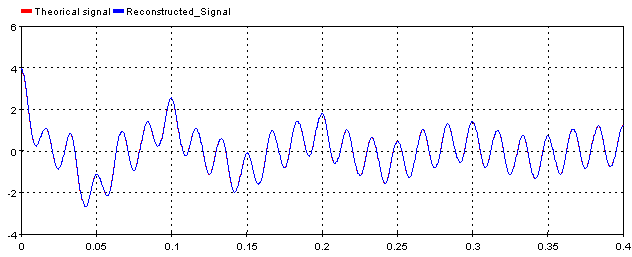
Model Reconstructed Signal	Input signal reconstructed with the dynamic parameters from the k complex mode identified in the analysis
Amplitude	Modal amplitude [ak]
Damping	Modal damping value [σk]
Frequency	Modal frequency [fk]
Phase	Phase shift [ϴk]
Damping Ratio	Modal relative damping ratio [ζk]
Signal	The input signal to be analyzed
Low Frequency	Low-frequency limit for oscillatory modes for the input signal. This limit must be set so there is at least a complete period in the window selected for analysis.

It must respect the following:

High Frequency: High-frequency limit for oscillatory modes for the input signal. It must be defined in a way so undersampling is avoided:

Amplitude Limit: Proportional maximum between the highest and lowest amplitudes of oscillatory mode displayed.

Damping Ratio Limit: Minimum relative damping of oscillatory modes displayed.

Trigger Time	Time at which the analysis begin. It must be determined in a way that at least a period of Low Frequency is observable. The starting time will be floored to the first sample available.
Model Order	Number of elements kept for the minimal realization of ERA.
0	Model order is automatically set with the singular values decomposition evaluation of the Hankel matrix.
Greater than 0	Model order is manually set to this value. However if the chosen order is greater than the maximal order permitted for the computation of Hankel matrix, the order will be set automatically.
Filtering Mode (optional) [On =1 , Off = 0]	Define if bandpass filter is applied or not. Low and High Frequency parameters will define the cutoff frequencies.

SYNTAX
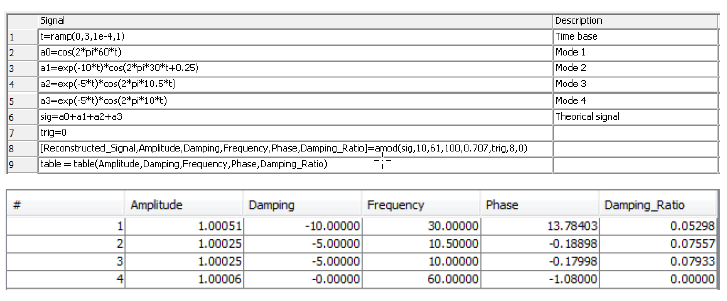
[Reconstructed_Signal,Amplitude,Damping,Frequency,Phase,Damping_Ratio]=amod(sig,Low_Freq,High_Freq,Amp_Lim,Damp_R_Lim,Trig,8,0)
Note that 8 is the Order and 0 is the filter. Since these only accept integer value, parameters cannot be set by variable.

CHARACTERISTICS
Data type support
Double Floating point
Integer for Model Order and Filtering Mode

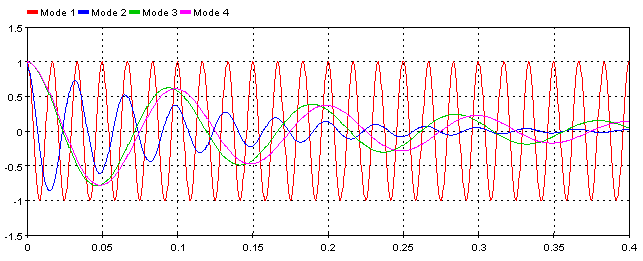
EXAMPLE
For this example, a simple signal is constructed with ScopeView